Search Algorithm

搜索算法简述

分类

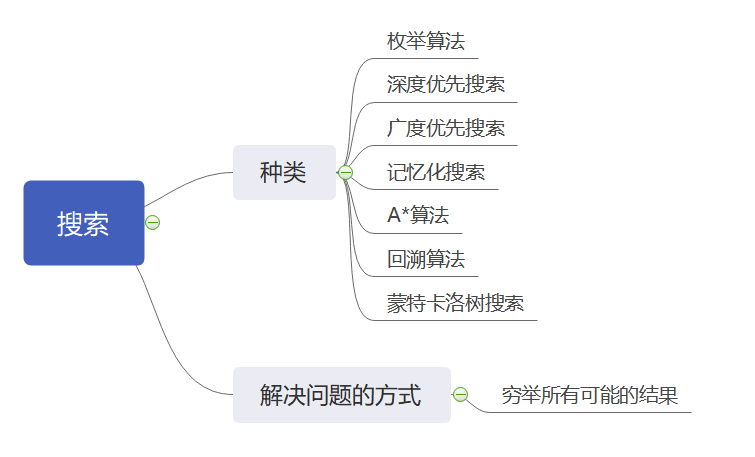
• 扩展阅读：蒙特卡洛树搜索最通俗入门指南 - 知乎

回溯与DFS

递归树

• 此处所举例子：实现1~3全排列

  • 最简单实现：三层循环+一个条件判断
  • 高阶：回溯；vis[]数组

• 通用性模板：

  void dfs(){
      if(){}	//递归终止条件
      if(){}	//剪枝优化条件
      
      for(){	//深搜
          //状态标记
  		dfs()
          //状态恢复：这里进行回溯，需要设置状态标记
      }
  }

A*

基础款介绍

伪码

• 启发式算法：
  • 估值函数：f(n)=g(n)+h(n)，注意对启发部是有限制条件

while(OPEN!=NULL)
{
    从OPEN表中取f(n)最小的节点n;
    if(n节点==目标节点)
        break;
    for(当前节点n的每个子节点X)
    {
        计算f(X);
        if(XinOPEN)
            if(新的f(X)<OPEN中的f(X))
            {
                把n设置为X的父亲;
                更新OPEN表中的f(n);
            }
        if(XinCLOSE)
            continue;
        if(Xnotinboth)
        {
            把n设置为X的父亲;
            求f(X);
            并将X插入OPEN表中;//还没有排序
        }
    }//endfor
    将n节点插入CLOSE表中;
    按照f(n)将OPEN表中的节点排序;//实际上是比较OPEN表内节点f的大小，从最小路径的节点向下进行。
}//endwhile(OPEN!=NULL)

设计

• open集与close集：

• 操作

  $$open=\left{
  \begin{matrix}
  delete \
  insert
  \end{matrix}
  \right.
  $$

• 会退化为Dijkstra：

  • A*详解 译文
  • A*能否最优解

增强款介绍

1.LPA

2.D*

• 相关阅读D* - Wikiwand

扩展阅读：D*

优化策略

剪枝：最优性剪枝

实际即为上下界限制的剪枝

• 剪枝策略本身包括：1. 可行性剪枝$\rightarrow$能否得到可行的解 2.最优性剪枝$\rightarrow$当前结点无法产生更优解时可提前回溯

​

算法知识扩展

启发式算法

最优化算法与启发式算法

• 扩展阅读：常见的几种最优化方法

算法收敛性与收敛速度

• 扩展阅读：浅谈算法收敛性与收敛速度

在线算法与离线算法

• 在线算法

  可能不是最优解

Dijkstra相关证明

• 数学归纳+极限思想