随机过程与计数过程

Stochastic Process Intro

概念

随机过程:

是依赖于参数的一组随机变量的全体，参数通常是时间。随机变量是随机现象的数量表现，其取值随着偶然因素的影响而改变。

主要内容有：多指标随机过程、无穷质点与马尔可夫过程、概率与位势及各种特殊过程的专题讨论等。

简介

马尔可夫过程

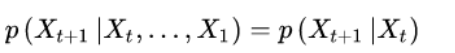
关键词

1. 随机变量
2. 状态空间(可数集)
3. 指数集(通常也即"步"/“时间步”)
4. 马尔可夫性质也即：“无记记忆性”。 满足马尔可夫性质即马尔可夫过程，其中离散马尔可夫过程称(具有马尔可夫性质的一组离散随机变量集合)马尔可夫链。
5. t+1步的随机变量在给定第t步随机变量后与其余的随机变量条件独立

例如：股票涨跌模型

泊松过程，独立增量过程是马尔可夫过程

转移理论

转移概率与转移矩阵

参考资料：

• 百度百科-马尔可夫链

Counting Process Intro

概念

泊松过程与更新过程是重要计数过程。

定义

对于非负且取值为整数的随机过程N(t)，如果N(t)表示时间间隔[0，t]内事件发生的总数，并满足如下两条特性，则N(t)为计数过程：

1. 若t1<t2，则N(t1)≤N(t2)；
2. 若t1<t2，则N(t1)-N(t2)为时间间隔(t1，t2]间事件发生的总数。
   例如，如果N(t)表示在t时刻之前进入一家饭店的人数，那么N(t)就是计数过程，只要有人进入饭店事件就会发生

泊松过程与泊松点过程

• 根据不同维度可分一维、二维、三维等
• 即有时间泊松过程与空间泊松过程

泊松过程

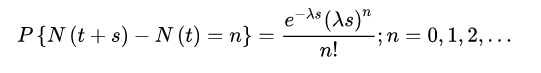
泊松点过程

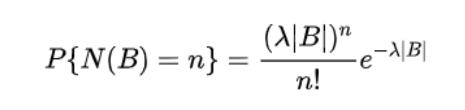
扩展

1. 泊松分布、正态分布非常常见。

2. 常见用法有：空间上的泊松点过程，时间上的正态分布变化以及时间上的泊松过程。

参考文献：

• 空间点过程与随机测度
• 百度百科-计数过程
• 正态分布的运用
• 泊松点过程
• 百度百科-伯努利实验