Data Structure by CSKaoYan

阅读量

树

二叉树

题目

一、通过前序遍历与中序遍历确定一棵二叉树

这代码还有问题，目前输出的还是前序遍历，明天再看一下，先去洗个澡。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// 输出层次遍历结果 
#include<stdio.h>

void traverseTree(char pre[], char in[], int preLeft, int preRight, int inLeft, int inRight){
	if(preLeft>preRight||inLeft>inRight) return;
	
	char root = pre[preLeft];
	printf("%c\n", root);
	
	// 中序遍历中查找根节点的下标 
	int index;
	for(int i=inLeft;i<=inRight;i++){
		if(in[i]==root){
			index=i;
			break;
		}
	}
	
	// 左子树 
	traverseTree(pre, in, preLeft+1, preLeft+index-inLeft, inLeft, index-1);
	// 右子树 
	traverseTree(pre, in, preRight-inRight+index+1, preRight, index+1, inRight);
}
int main(){
	/*char pre[]={'A', 'D', 'B', 'C', 'E'};
	char in[]={'B', 'D', 'C', 'A', 'E'};	
	traverseTree(pre, in, 0, 4, 0, 4);*/
	
	char pre[]={'D','A','E','F','B','C','H','G','I'};
	char in[]={'E','A','F','D','H','C','B','G','I'};
	traverseTree(pre, in, 0, 8, 0, 8);
}

线索二叉树的概念

线索二叉树的作用

  • 主要用于遍历序列
  • 方便找前驱、后继以及遍历

包括先序遍历、中序遍历、后序遍历线索二叉树

【线索】指向前驱、后继的指针称为线索

线索二叉树的存储结构

二叉链表-线索链表

1
2
3
4
5
struct Node{
	int val;
	struct Node *left, *right;
	int ltag, rtag;  // tag=1表示是指向为线索
};

二叉树的线索化

1
2
3
4
5
6
7
8
9
10
11
12
13
/* 土法找到中序前驱 */
void inOrder(Node* root){
	if(root == nullptr) return;
	inOrder(root->left);
	vist(root);
	inOrder(root->right);
}
// 在vist中完成线索化，只有在访问时才操作（访问序列）
void vist(Node* node){  
	if(node == final) return pre;
	else pre = node;
	printf("%d", node->val);
}

在线索二叉树中找前驱后继

树的存储结构

  1. 树是一种递归定义的数据结构

  2. 存储结构

双亲表示法 孩子表示法 孩子-兄弟表示法
存储结构 顺序存储 顺序+链式(邻接表) 链式
增 nodes[idx++]=node - -
删 ①nodes[k].p=-1或swap(node[idx],node[k]);②遍历全表删除p=k的子孙节点 - - 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/* 双亲表示法 */
struct Node{
	int val; // 值
	int p;   // 父亲的序号，-1表示没有
}node[N];    // 数组，第一个固定表示根节点(index=0)
struct Tree{
	Node nodes[N];
	int num;
};

/* 孩子表示法 */
struct Child{
	int val;
	struct Child* p;
};
struct Node{
	int val
	struct Child* first;
};
struct Tree{
	Node nodes[N];
	int n, r;     // n为节点数，r为根位置
};

/* 孩子-兄弟表示法 */
struct Node{
	int val;
	struct Node *child, *p; // 左孩子右兄弟
};

树与森林的遍历

二叉树 树 森林
先序遍历 先序遍历 先序遍历
中序遍历 后序遍历 中序遍历

🌸二叉排序树

默认不允许两个节点关键字相同

💖3595.二叉排序树-要求返回父节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int n, root;
unordered_map<int, int> l, r;
// 建立BST
int dfs(int f, int x){
	if(f==-1){
		root=x;
		return -1;
	}
	if(x > f){
		if(!r.count(f)){
			r[f] = x;
			return f;
		}
		else return dfs(r[f]);
	}
	if(x < f){
		if(!l.count(f)){
			l[f] = x;
			return f;
		}
		else return dfs(l[f], x);
	}
}
// 中序遍历BST
void visit(int root){
	if(!l.count(root)&&!r.count(root)){
		cout<<root<<endl;
		return;
	}
	
	if(l.count(root)) visit(l[root]);
	cout<<root<<endl;
	if(r.count(root)) visit(r[root]);
}

root = -1;
cout<<dfs(root, x)<<endl;
visit(root);

BST查找

迭代与递归

BST插入与构造

查找效率分析

ASL：最好情况，n个节点的BST最小高度为

平衡二叉树

平衡因子：左子树高-右子树高 -> {-1,0,1}

调节BST至AVL

调整最小不平衡子树：LL,RR,LR,RL

查找效率分析

哈夫曼树

带权路径长度

  1. 节点的权：某种特定含义的数值
  2. 节点的带权路径长度：根到节点路径长度 * 节点的权值
  3. 树的带权路径长度(WPL) = 树中所有叶子节点的带权路径长度之和

    哈夫曼树定义

  • 最优二叉树：在含有给定的n个叶子节点的二叉树中，WPL最小的二叉树
  • 不存在度为1的节点
  • 完全二叉树。总节点数：2n-1

哈夫曼树构造

（可以通过森林与集合对算法过程描述）

哈夫曼编码

  1. 固定长度编码
  2. 可变长度编码
  3. 前缀编码

图

查找

顺序查找

用于线性表

  1. 无序线性表：优化：a[0]设置哨兵
  2. 有序线性表：可优化查找失败ASL：查找判定树
    • 若被查到概率不同：可优化查找成功ASL

      折半查找

      用于顺序表

  3. 查找判定树
  4. 左右子树

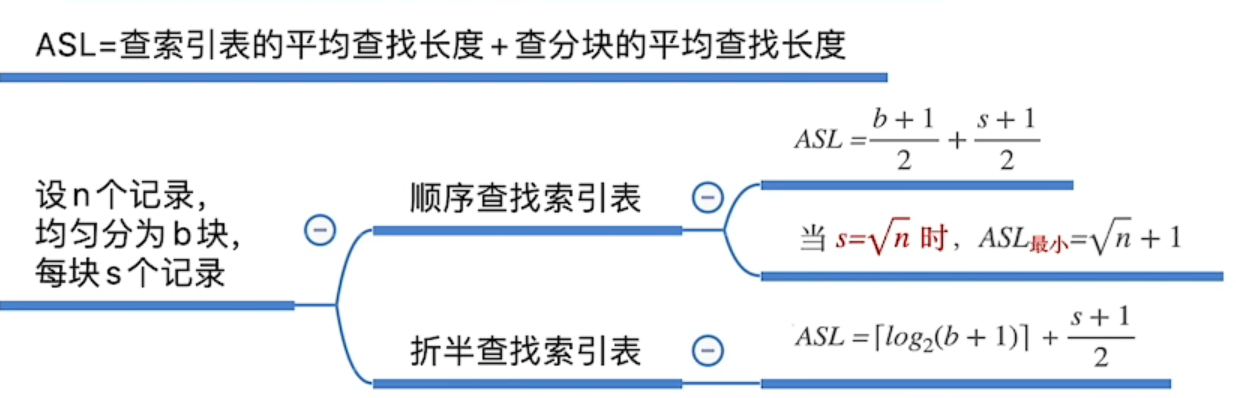
分块查找

索引顺序查找

1
2
3
4
5
6
7
// 索引表
typedef struct{
	int maxVal;
	int low, high;
};
// 顺序表存储实际元素
int List[N];
  • 扩展：动态查找表则可链式存储(否则静态数组仍需O(n)复杂度增删)
  1. 查找情况
  • 索引表查找：顺序查找与二分查找
  • 查找情况：
    • 索引表查到：直接返回
    • 索引表未查到：low>high，则low所指分块顺序查找；超出范围则失败
  1. ASL
    • 索引表折半：索引未查到也需一直二分
    • ASL = 索引查找ASL + 块内查找ASL

B树

多路平衡查找树；子树=关键字+1（关系）

最重要的：

  1. 对m阶B树，除根节点外，每个节点关键字数目：
  2. 若根节点不是终端节点，则至少有2个子树
  3. 子树0<关键字1<子树1<关键字2<…
  4. 树中每个节点至多有m个子树、即最多m-1个关键字
  5. 所有叶子节点都在同一层次上且不带信息（即完全绝对平衡）
  • 含有n个关键字的m叉B树的高度
    【最小高度】

记k=
| | 最少节点数 |最少关键字|
| :———–: | :———–: | :———–: |
|第一层|1|1|
|第二层|2|2(k-1)|
|第三层|2k|2k(k-1)|
|第四层|2k^2|2k^2(k-1)|
|…|…|…|
|第h层|2k^h-2|2k^h-2(k-1)|

B树的插入删除

  1. 插入

    • 只能插入到终端节点（满足叶子节点性质）
    • 节点数目超过上限时，进行分裂：选择节点插入到父节点合适位置维持有序性（可能持续分裂，根节点分裂将导致树高度+1）

  2. 删除

    • 终端关键字删除：
      • 未低于下限：无需处理
      • 低于下限：
        ①兄弟节点够借：需要变动前驱与前驱的前驱/后继与后继的后继
        ②兄弟节点不够借：将自己与兄弟节点、父节点关键字合并为一个节点（可能持续合并，合并到根节点会导致树高度-1）
    • 非终端关键字删除：
      • 类似BST删除，以直接前驱/直接后继进行替换。转化为终端关键字删除

B+树

对于一个m阶B+树：

  • 每个分支节点最多有m棵子树
  • 非叶根节点最少2棵子树，其余分支节点至少棵子树
  • 节点的子树个数与关键字个数相等
  • 叶子节点包含全部关键字及相应的指针，同时相邻叶节点按大小顺序链接起来（支持顺序查找）
  • （具有类似分块查找的性质）

查找：

  • B+：多路查找，分支仅起索引作用
  • 典型应用：MySQL索引。（相比B树不包含分支对应记录的存储地址，因此可以使得磁盘包含更多关键字，使树高更矮，读磁盘次数更少，查找效率更高）

散列查找

  1. 构造hash表
    • 除留余数法
    • 直接法
    • 数据分析法
    • 平方法
  2. 冲突处理
    • 拉链法
    • 开放定址法（线性探测、平方探测、伪随机数）
  3. 查找效率分析
    • 装填因子

排序

直接插入排序

  • 空间复杂度：O(1)
  • 时间复杂度：
    • 最好（有序）：O(n)
    • 最坏（逆序）/平均：O(n^2)
  • 稳定
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    void insert_sort(int q[]){
    	for(int i=1; i<n; i++){
    		int tmp=q[i], j=i;
    		while(j>0&&tmp<q[j-1]){ //注意
    			q[j]=q[j-1];
    			j--;
    		}
    		q[j]=tmp;
    	}
    }

    // 7 3 6 2 5 1
    int main(){
    	scanf("%d",&n);
    	for(int i=0; i<n; i++) scanf("%d",&q[i]);
    	
    	insert_sort(q);
    	
    	for(int i=0; i<n; i++) printf("%d ",q[i]);	
    }
  • 折半插入排序：将元素放到q[low]的位置后移[low,i-1]；相等元素q[low+1]=tmp
  • 链表插入排序

希尔排序(Shell Sort)

淦，在这里反复错了好多次然后才改对的

  • 时间复杂度：与d的选择有关；最坏情况退化为直接插入排序
  • 不稳定
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    void shell_sort(int q[]){
    	for(int d=n/2; d>=1; d/=2){
    		for(int i=1+d; i<=n; i++){
    			int tmp=q[i], j=i;
    			while(j>0&&tmp<q[j-d]){  // 这里错了一直没发现
    				q[j]=q[j-d];
    				j-=d;
    			}
    			q[j]=tmp;
    		}
    	}
    }
  • 只适用于顺序表：需要有增量d，因此需要有随机访问的特性

冒泡排序

  • 时间复杂度：
    • 最好情况（有序）：O(n)
    • 最坏情况（逆序）：O(n^2)
  • 未发生交换可以提前结束
  • 稳定
  • 链表

快速排序

  • 时间复杂度：
    • 若基准元素能够将区间划分为均匀两部分则效率最高
    • 若本身有序或逆序，则效率最低
  • 不稳定

补充： 二叉树最小高度：
；
最大高度：n

简单选择排序

  • 时间复杂度：在有序无序情况下运算情况一致，复杂度始终为o(n^2)
  • 不稳定
  • 链表

堆排序

  • 初始化等操作见另一blog
  • 时间复杂度：
    • 建堆：O(n)；排序：O(nlogn)
    • 总：O(nlogn)
  • 不稳定

归并排序

  • 空间复杂度：O(n)
  • 时间复杂度：O(nlogn)
  • 稳定

基数排序(Radix Sort)

  • 唯一不是基于比较的排序；使用关键字进行排序
  • 用于链式存储结构
    1
    2
    3
    4
    5
    6
    7
    8
    9
    // 表示每一个元素
    struct Node{
    	int val;
    	struct Node* next;
    };
    // 队列
    struct{
    	struct Node* head, tail;
    }q[N];
  • 空间复杂度：O(r)
  • 时间复杂度：
    • 分配：O(n)，收集：O(r)；总共d趟分配收集，所以总时间复杂度O(d(n+r))
  • 稳定
  • 适用问题：
    • 关键字可以拆分为d组，且d较小
    • 每组关键字取值范围不大，即r较小
    • 数据个数n较大

外部排序

归并排序–优化：多路归并（增加输入缓冲区）

Powered by Hexo and Hexo-theme-hiker

Copyright © 2013 - 2022 Bowlmeat's Blogs All Rights Reserved.

访客数 : | 访问量 :