Graph

阅读量

DFS

842.排列数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void dfs(int u){
    if(u > n){
        for(int i=1; i<=n; i++)
            printf("%d ", path[i]);
        printf("\n");
        return;
    }
    for(int i=1; i<=n; i++){
        if(!st[i]){
            st[i]=true;
            path[u]=i;
            dfs(u+1);
            st[i]=false;
        }
    }
}
dfs(1);  // 调用

843.n-皇后问题
对角线的表示最为巧妙

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int path[N];
void dfs(int u){
    if(u>=n){
        for(int i=0; i<n; i++){
            for(int j=0; j<n; j++){
                if(path[i]==j) printf("Q");
                else printf(".");
            }
            printf("\n");
        }
        pritntf("\n");
    }

    for(int i=0; i<n; i++){
        if(!col[i]&&!dg[u+i]&&!ndg[u-i+n]){
            col[i] = dg[u+i] = ndg[u-i+n] = 1;
            path[u] = i;
            dfs(u+1);
            col[i]= dg[i+u] = ndg[u-i+n] = 0;
        }
    }
}

dfs(0); //调用

BFS

844.走迷宫
坐标转化方面总出问题
合法性检测！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int q[N], head=0, tail=-1, d[N];

q[++tail]=1;
while(head<=tail){
    int u = q[head++];
    int xu = (u-1)/m + 1, yu = u - (xu-1)*m;
    for(int i=0; i<4; i++){
        int xx = xu + dx[i], yy = yu + dy[i];  // 坐标转化1
        int loc = (xx-1)*m + yy;    //2
        if(xx>m||xx<1||yy>m||yy<1) continue; // 忽略合法性检测
        if(!d[loc]&&!map[xx][yy]){
            q[++tail]=loc, d[loc]+=d[u];
        }
    }
}
printf("%d", d[m*n]);

845.八数码

求最短路/最短距离->BFS
(长见识了：康托展开和逆康托展开)

我的艰辛历程：字符哈希–结果没法逆回来×；头铁一定要纯C自己写队列×

string的API使用：

①string.find()

②这里必须使用二维坐标表示，一维错误

③t重复使用需要两次swap

④合法性检查

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int bfs(string start){
    string end = "12345678x";
    
    queue<string> q;
    unordered_map<string, int> d;
    q.push(start);
    d[start] = 0;
    
    while(!q.empty()){
        auto t = q.front();
        q.pop();             // 忘记了
        
        int dis = d[t];
        
        if(t == end) return dis;
        
        int x = t.find('x');
        int xx = x/3, yy = x%3;
        int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0};
        for(int i=0; i<4; i++){
            int nx = xx + dx[i], ny = yy + dy[i];
            if(nx<0||nx>2||ny<0||ny>2) continue;
            swap(t[x], t[3*nx+ny]);
            if(!d.count(t)){        //unordered_map使用的极易错点
                d[t] = dis + 1;
                q.push(t);
            }
            swap(t[x], t[3*nx+ny]);   // 这里！
        }
    }
    return -1; // 忘记了
}

int main(){
    string start;
    for(int i=0; i<9; i++){   // 这个输入很灵性
        char t;
        cin>>t;
        start += t;
    }
    cout<<bfs(start)<<endl;
}

树与图的深度优先遍历

存储结构

图：邻接矩阵（用的少），邻接表

树的DFS

🌺846.树的重心
(就目前我的水平来说整个代码都是重点–)

几个常犯错误： 1.memeset(h, -1, sizeof h) 2.st[]使用：通常都会有

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int h[N], e[N], ne[N], idx;
bool st[N];
int ans;

void add(int a, int b){
    e[idx]=b, ne[idx]=h[a], h[a]=idx ++;
}

int dfs(int x){
    // 这里记得存个疑（一般都会有st限制为仅遍历一次
    st[x] = true; 
    int sum = 1, res = 0;
    for(int i=h[x]; i!=-1; i=ne[i]){
        int u = e[i];
        if(!st[u]){  // 猜测约束为树的遍历
            int s = dfs(u);
            res = max(res, s);
            sum += s;
        }
    }
    res = max(res, n-sum);
    ans = min(ans, res);

    return sum;
}

int main(){
    scanf("%d", &n);
    memset(h, -1, sizeof h);  //容易忘记

    for(int i=0; i<n; i++){
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }
    dfs(1);
    return ans;
}

图的BFS

847.图中点的层次
常犯错误：经常把idx给存到queue里

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int q[N], tt, hh;
int h[N], e[N], ne[N], idx;
int d[N];

memset(h, -1, sizeof h);
memeset(d, -1, sizeof h);

hh = 0, tt = -1;
q[++tt] = 1;
d[1] = 0;
while(hh <= tt){
    int u = q[hh++];

    for(int i=h[u]; i!=-1; i=ne[i]){
        int t = e[i];
        if(d[t]==-1){
            q[++tt] = t;
            d[t] = d[u] + 1;
        }
    }
}
printf("%d", d[n]);a

拓扑序列

1.某种程度上的BFS； 2.抽屉原理证明有向无环图性质；

1
2
3
4
5





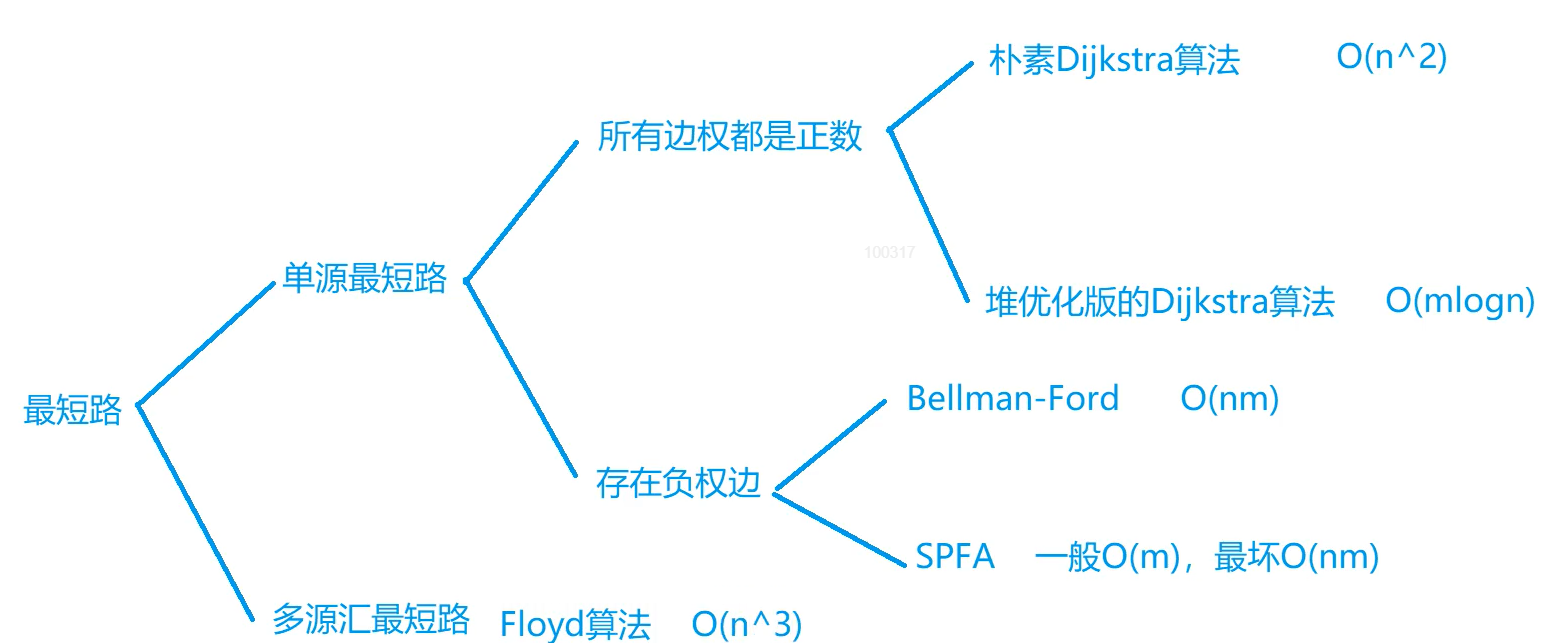
最短路问题

单源最短路

朴素Dijkstra

O(n^2)

🍉带佬说： 不能解决负权是因为dijkstra要求每个点被确定后st[j] = true，dist[j]就是最短距离了，之后就不能再被更新了（一锤子买卖），而如果有负权边的话，那已经确定的点的dist[j]不一定是最短了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int djikstra(){
    memset(d, 0x3f, sizeof d);
    d[1] = 0;

    for(int i=0; i<n; i++){
        int t = -1;
        for(int j=1; j<=n; j++){
            if(!st[j]&&(t==-1||d[j]<d[t])) t=j;  //没访问+最短
        }
        st[t] = 1;

        for(int j=1; j<=n; j++){
            if(d[j]>d[t]+g[t][j]) d[j]=d[t]+g[t][j];
        }
    }
    if(d[n]==0x3f3f3f3f) return -1;
    else return d[n];
}

堆优化Dijkstra

优先队列，O(mlogn)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
typedef pair<int, int> PII;
int h[N], w[N], e[N], ne[N], idx;
int st[N], d[N];


void dijkstra(){
    memset(d, 0x3f, sizeof d);

    priority_queue<PII, vector<PII>, greater<PII>> q;
    q.push({0, 1});
    d[1]=0;

    while(!q.empty()){
        int t = q.top(), q.pop();
        int ver = t.second;

        if(st[ver]) continue;
        st[ver] = 1;
        for(int i=h[ver]; i!=-1; i=ne[i]){
            int u = e[i], wt = w[i];
            if(d[u]>d[ver]+wt){
                d[u]=d[ver]+wt;
                q.push({d[u], u});
            }
        }
        if(d[n] == 0x3f3f3f3f) return -1;
        else return d[n];
    }
}

Bellman-Ford

backup数组、struct结构体

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int d[N], backup[N];
struct Edge{
    int a, b, w;
}edge[M];

void bellman_ford(){
    memset(d, 0x3f, sizeof d);
    d[1] = 0;

    for(int i=0; i<k; i++){
        memcpy(backup, d, sizeof d);
        for(int j=0; j<m; j++){
            int a = edge[j].a, b = edge[j].b, wt = edge[j].w;
            if(d[b]>backup[a]+wt){
                d[b] = backup[a] + wt;
            }
        }
    }

    if(d[n] > 0x3f3f3f3f / 2) puts("impossible");
    else printf("%d\n", d[n]);
}

🍅SPFA

1.st[N]数组
2.唯一限制：有负环时不可使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void spfa(){
    memset(d, 0x3f, sizeof d);

    queue<int> q;
    q.push(1);
    d[1]=0, st[1]=1;

    while(!q.empty()){
        int t = q.front(); q.pop();
        st[t] = 0;

        for(int i=h[t]; i!=-1; i=ne[i]){
            int u = e[i], wt = w[i];
            if(d[u]>d[t]+wt){
                d[u] = d[t] + wt;
                if(!st[u]){
                    st[u] = 1;
                    q.push(u);
                }
            }
        }
    }
    if(d[n] == 0x3f3f3f3f) puts("impossible");
    else printf("%d\n", d[n]);
}

852. spfa判断负环

cnt[N]代表含义为边数（不是节点数）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void spfa(){
    queue<int> q;
    for(int i=1; i<=n; i++){  //将所有点压入队列
        q.push(i);
        st[i] = 1;   
    }

    while(!q.empty()){
        int t = q.front(), q.pop();
        st[t] = 0;
        
        for(int i=h[t]; i!=-1; i=ne[i]){
            int u = e[i], wt = w[i];
            if(d[u]>d[t]+wt){
                d[u]=d[t]+wt;
                cnt[u]=cnt[t]+1;

                if(cnt[u]>=n) return false;  // 边数判断
                if(!st[u]){
                    st[u] = 1;
                    q.push(u);
                }
            }
        }
    }
    return true;
}

多源汇最短路

Floyd

初始化数据为邻接矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
const int N = 210, INF = 0x3f3f3f3f;
int n, m, num;
int g[N][N];

void floyd(){
    for(int k=1; k<=n; k++)
        for(int i=1; i<=n; i++)
            for(int j=1; j<=n; j++)
                g[i][j] = min(g[i][k] + g[k][j], g[i][j]);
}

// 初始化
for(int i=1; i<=n; i++){
    for(int j=1; j<=n; j++){
        if(i==j) g[i][j]=0;
        else g[i][j] = INF;
    }
}

while(m--){
    int a, b, c;
    scanf("%d%d%d", &a, &b, &c);
    g[a][b] = min(g[a][b], c);
}
floyd();
while(num--){
    int a, b;
    scanf("%d%d", &a, &b);
    if(g[a][b] > INF / 2) puts("impossible");
    else printf("%d\n", g[a][b]);   
}

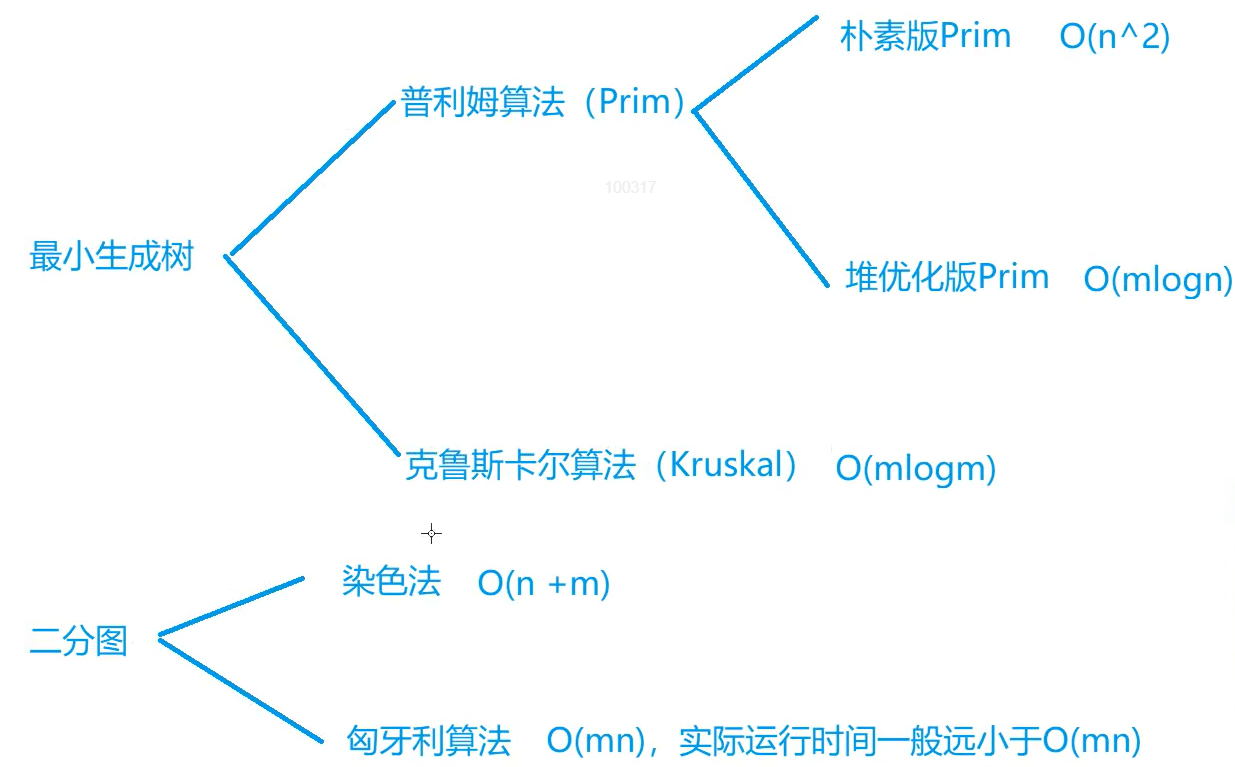
最小生成树

🍎朴素Prim

错了好几个地方： 1. 第一个节点特殊处理 2. 非第一节点d[t]==INF时则不连通 3. 求pre时松弛需要判断st[i]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void prim(){
    memset(d, 0x3f, sizeof d);

    int res = 0;
    for(int i=0; i<n; i++){
        int t=-1;
        for(int j=1; j<=n; j++){
            if(!st[j]&&(t==-1||d[j]<d[t])) t=j;
        }
        st[t] = 1;

        if(i&&d[t]==INF){
            puts("impossible");
            return;
        } 
        if(i) res += d[t];

        for(int j=1; j<=n; j++){  // 如果要pre[]数组，
            if(d[j]>g[t][j]) d[j] = g[t][j];  // 则if条件要强化为再添加!st[j]。-> pre[j]=t
        }
    }
}

堆优化Prim

太复杂，不使用；稀疏图使用Kruskal

Kruskal

1.再强调一下重载运算符（重载小于号）：（偏序关系）
sort中的cmp函数与优先队列priority_queue的重载函数重载小于号

🍄2.并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
struct edge{
    int a, b, w;
    bool operator < (const Edge& e) const{
        return w < e.w;
    }
}edge[M];

for(int i=1; i<=n; i++) p[i] = i;
for(int i=0; i<m; i++){
    int a, b, w;
    cin>>a>>b>>w;
    edge[i] = {a, b, w};
}

sort(edge, edge+m);
int res = 0, cnt = 1;
for(int i=0; i<m; i++){
    int a=edge[i].a, b=edge[i].b, w=edge[i].w; 
    if(find(a)==find(b)) continue;
    else{
        res+=w, cnt++;
        p[find(a)] = find(b);
    }
}
if(cnt!=n) cout << "impossible"<<endl;
else cout << res <<endl;

二分图

染色法

常犯错误: 没写int t=e[i]; --> 分清idx

递归深搜yyds!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int color[N];

bool dfs(int u, int c){
    color[u] = c;
    for(int i=h[u]; i!=-1; i=ne[i]){
        int t = e[i];
        if(!color[t]){
            if(!dfs(t, 3-c)) return false;
        }
        else if(color[t]!=3-c) return false;
    }
    return true;
}

for(int i=1; i<=n; i++){
    if(!color[i]){
        if(!dfs(i, 1)){
            cout << "No" << endl;
            return;
        }
    }
}
cout << "Yes" << endl;

⭐ 匈牙利算法

🍊 861.二分图的最大匹配
好几个错的：1. st[N]数组使用 2. e[M] 3. 递归思想

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
const int N=510, M=100010;
int h[N], e[M]. ne[M], idx;
int match[N], st[N];
int n1, n2, m;

bool find(int u){
    for(int i=h[u]; i!=-1; i=ne[i]){
        int t=e[i];
        if(!st[t]){
            st[t]=1;    // 注意位置
            if(!match[t]||find(match[t])){   // 递归
                match[t] = u;
                return true;
            }
        }
    }
    return false;
}

int main(){
    cin >> n1 >> n2 >> m;

    while(m--){
        int a, b;
        cin >> a >> b;
        add(a, b);
    }

    int res = 0;
    for(int i=1; i<=n1; i++){
        memset(st, 0, sizeof st);  // 老忘记
        if(find(i)) res++;
    }
    cout << res << endl;
}

🍊372.棋盘覆盖

先染色判断二分图情况

Powered by Hexo and Hexo-theme-hiker

Copyright © 2013 - 2022 Bowlmeat's Blogs All Rights Reserved.

访客数 : | 访问量 :