Basic Algorithms

阅读量

排序

快速排序

  • 分治，确定分界点-调整区间-递归左右，不稳定
  • 很多边界问题
    1. x=q[l]; -> quicksort(q, l, j); quicksort(q, j+1, r);
    2. x=q[r]或者x=q[(l+r+1)/2]; -> quicksort(q, l, i-1); quicksort(q, i, r);
    3. 避免一直取到左边界或者右边界
  • 调整区间的简单思想：额外开两个数组，左边放一个右边放一个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
const int N = 1e6 +  10;
int q[N], n;

void quick_sort(int q[], int l, int r){
    if(l >= r) return;    // 1.结束递归条件

    int x = q[l], i = l-1, j = r+1;  // 2.基准，左，右
    while(i < j){
        do i++; while(q[i]<x);
        do j--; while(q[j]>x);
        if(i<j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j);  // 3. 见上；边界
    quick_sort(q, j+1, r);
}

int main(){
    scanf("%d", &n);
    for(int i=0; i<n; i++)  scanf("%d", q[i]);

    quick_sort(q, 0, n-1);
}
  • 变形：【找出第k个数】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;

const int N = 100010;
int n, k;
int a[N];

int quick_sort(int l, int r){
    if(l >= r) return a[k];
    
    int i = l-1, j = r+1, x = a[l];
    while(i < j){
        do i++; while(a[i] < x);
        do j--; while(a[j] > x);
        if(i < j) swap(a[i], a[j]);
    }
    
    if(j >= k) return quick_sort(l, j);
    else return quick_sort(j+1, r);
}

int main(){
    cin >> n >> k;
    for(int i=0; i<n; i++) cin >> a[i];
    
    k--;
    cout << quick_sort(0, n-1);
}

归并排序

  • 分治，确定分界点-递归左右-合二为一，稳定

我真的会谢）典错误：写最后的合并的时候顺手加上了自增其实不应该

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
const int N = 100010;
int q[N], tmp[N];
int n;

void merge_sort(int q[], int l, int r){
    if(l >= r) return;
    int mid = l + r >> 1;

    merge_sort(q, l, mid), merge_sort(q, mid+1, r);

    int i=l, j=mid+1, k=l;
    while(i<=mid&&j<=r){
        if(a[i]<=a[j]) tmp[k++] = a[i++];
        else tmp[k++] = a[j++];
    }
    while(i<=mid) tmp[k++] = a[i++];
    while(j<=r) tmp[k++] = a[j++];

    for(int i=l; i<=r; i++) a[i] = tmp[i]; // 这儿
}

int main(){
    scanf("%d", &n);
    for(int i=0; i<n; i++) scanf("%d", &a[i]);
    
    merge_sort(q, 0, n-1);
    for(int i=0; i<n; i++) printf("%d ", a[i]);
}

查找

🍨整数二分

核心思想

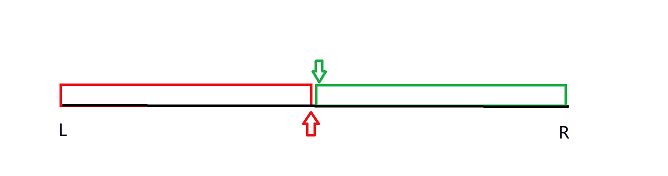
  1. 初始化：l=0, r=n-1;
  2. 查找红色区域右边界：
    1
    2
    3
    4
    5
    while(l < r){
        mid = l + r + 1 >> 1;
        if(check(mid)) l = mid;
        else r = mid - 1;
    }
  3. 查找绿色区域左边界：
    1
    2
    3
    4
    5
    while(l < r){
        mid = l + r >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }
  4. check函数的设计
  5. 无解情况

789.数的范围

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int a[N], n, q;

int main(){
    cin >> n >> q;
    for(int i=0; i<n; i++) cin >> a[i];

    while(q--){
        int k; cin >> k;

        int l = 0, r = n-1, mid;
        while(l < r){
            mid = l + r >> 1;
            if(a[mid] <= k) r = mid;
            else l = mid + 1;
        }
        if(a[l] != k) cout << "-1 -1" << endl;
        else{
            cout << l << " ";

            l = 0, r = n-1;
            while(l < r){
                mid = l + r + 1 >> 1;
                if(a[mid] >= k) l = mid;
                else r = mid - 1;
            }
            cout << r << endl;
        }
    }
}

🍰3712.根能抵达的点
二分搜索查找 + 树的dfs
(还存在问题，虽然我不李姐为啥)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<stdio.h>
#include<string.h>
const int N = 20010, M = 2*N;
int h[N], e[M], ne[M], w[M], idx;
int n, y;

void add(int u, int v, int wt){
	e[idx]=v, w[idx]=wt, ne[idx]=h[u], h[u]=idx++;
}

int dfs(int u, int mid, int f){
	int res = 1;
	for(int i=h[u]; i!=-1; i=ne[i]){
		if(e[i]!=f&&w[i]>mid) res += dfs(e[i], mid, u);
	}
	return res;
}

int main(){
	int T;
	scanf("%d", &T);
	while(T--){
		scanf("%d%d", &n, &y);
		
		memset(h, -1, sizeof h); idx=0;
		int u, v, wt;
		for(int i=0; i<n-1; i++){
			scanf("%d%d%d", &u, &v, &wt);
			add(u, v, wt), add(v, u, wt);
		}
		
		int l= 0, r = 1e8;
		while(l<r){
			int mid = l + r >> 1;
			if(dfs(0, mid, -1)<=y) r = mid;
			else l = mid + 1;
		}
		printf("%d\n", r);	
	}	
}

浮点数二分

790.数的三次方根

错两位；特殊在左右边界给定

1
2
3
4
5
6
7
8
9
10
11
12
int main(){
	double n;
	scanf("%d", &n);
	
	double l = -10000, r = 10000;
	while(r - l > 1e-8){
		double mid = (l + r) / 2;
		if(mid*mid*mid>n) r = mid;
		else l = mid;
	}
	printf("%.6lf", l);
}

高精度

加法

791.高精度加法

输入一个$\frac{a}{b}$

减法

乘法

除法

前缀和

一维

  • 求前缀和公式：
  • 求区间和公式：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
const int N = 100010;
int a[N], s[N];
int n, m;

int main(){
    scanf("%d", &n, &m);
    for(int i=1; i<=n; i++){
        scanf("%d", &a[i]);
        s[i] = s[i-1] + a[i];
    }

    int l, r;
    while(m--){
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r]-s[l-1]);
    }
}

二维

差分

一维

二维

双指针

  • 逻辑框架
    1
    2
    3
    4
    for(int i=0, j=0; i<n; i++){
        while(j<i && check(i,j)) j++;
        // 具体逻辑
    }
    799.最长连续不重复子序列

有点滑动窗口的感觉，涉及到单调性

  • 数据大/字母则hash
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const int N = 100010;
int s[N], a[N];
int n;

int main(){
    scanf("%d", &n);
    for(int i=0; i<n; i++) scanf("%d", &a[i]);

    int res = 1;
    for(int i=0, j=0; i<n; i++){
        s[a[i]]++;        // 注意这几个自增自减的次序
        while(s[a[i]]!=1){
            s[a[j]]--;
            j++;
        }
        if(i-j+1>res) res = i - j + 1;
    }
    printf("%d",res);
}

位运算

  • x >> k & 1：求n的第k位数字（0<=k<=n-1）
  • lowbit(n) = x & -x：返回n的最后一位1

离散化

  • 过程：
    1. vector<int> alls; 存储所有待离散化数值
    2. sort(alls.begin(), alls.end()); 排序
    3. alls.erase(unique(alls.begin(), alls.end()), alls.end()) 去重
    4. 二分确定index
  • unique函数自实现：
1
2
3
4
5
6
vector<int>::iterator unique(vector<int>& a){
    for(int i=0, j=0; i<a.size(); i++){
        if(!i || a[i]!=a[i-1]) a[j++] = a[i];
    }
    return a.begin() + j;
}
  • 离散化

802.区间和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

const int N = 300010;
int a[N], s[N];
int n, m;

typedef pair<int, int> PII;
vector<PII> adds, querys;
vector<int> alls;

int find(int x){   // 映射：a[index]->index
	int l = 0, r = alls.size() - 1;
	while(l < r){
		int mid = l + r >> 1;
		if(alls[mid]>=x) r=mid;
		else l=mid + 1;
	}
	return l+1;
}

int main(){
	cin >> n >> m;
	
	for(int i=0; i<n; i++){
		int x, c;
		cin >> x >> c;
		adds.push_back({x, c});
		alls.push_back(x);
	}
	
	for(int i=0; i<m; i++){
		int l, r;
		cin >> l >> r;
		querys.push_back({l, r});
		alls.push_back(l), alls.push_back(r);
	}
	
	sort(alls.begin(), alls.end());
	alls.erase(unique(alls.begin(), alls.end()), alls.end());
	
	for(int i=0; i<adds.size(); i++){
		auto x = adds[i].first, c = adds[i].second;
		a[find(x)] += c;
	}
	
	for(int i=1; i<=alls.size(); i++){
		s[i] = s[i-1] + a[i];
	}
	
	for(int i=0; i<querys.size(); i++){
		int l=querys[i].first, r=querys[i].second;
		cout << s[find(r)] - s[find(l)-1] << endl;
	}
}

区间合并

803.区间合并
注意这个地方有点问题，虽然我整体思路什么的都是一致的但是发生了玄学问题，后续解决一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

const int N = 100010;
int n;

typedef pair<int, int> PII;

int main(){
	cin >> n;
	vector<PII> segs, res;
	int l, r;
	while(n--){
		cin >> l >> r;
		segs.push_back({l, r});
	}
	
	sort(segs.begin(), segs.end());
	int st=-1e10, ed=-1e10;
	for(auto seg : segs){
		int l=seg.first, r=seg.second;
		if(ed<l){
			if(ed!=-1e10) res.push_back({st, ed});
			st=l, ed=r;
		}
		else ed = max(ed, r);
	}
	if(ed!=-1e10) res.push_back({st, ed});
	cout << res.size()-1 << endl;  //就这
}

动态规划

背包问题

  • 01背包： 每件物品最多只用一次
  • 完全背包： 每件物品有无限个
  • 多重背包（优化）： $s_i$个
  • 分组背包： $N$组

(1) 01背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<iostream>
#include<algorithm>
const int N = 1010;
int n, m;
int v[N], w[N], f[N][N];

int main(){
    cin >> n >> m;
    for(int i=1; i<=n; i++) cin >> v[i] >> w[i];

    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            f[i][j] = f[i-1][j];
            if(j>v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i]);  // 容量是否够装i
        }
    }
    cout << f[n][m];
}

优化后： 滚动数组

1
2
3
4
int f[N];
for(int i=1; i<=n; i++)
    for(int j=m; j>=v[i]; j--)
        f[j] = max(f[j], f[j-v[i]]+w[i]);

(2) 完全背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<iostream>
#include<algorithm>
const int N = 1010;
int n, m;
int v[N], w[N], f[N][N];

int main(){
    cin >> n >> m;
    for(int i=1; i<=n; i++) cin >> v[i] >> w[i];

    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            for(int k=0; k*v[i]<=j; k++)
            f[i][j] = max(f[i][j], f[i-1][j-k*v[i]] + k*w[i]);
        }
    }
    cout << f[n][m];
}

优化后： 

1
2
3
4
int f[N];
for(int i=1; i<=n; i++)
    for(int j=v[i]; j<=m; j++)
        f[j] = max(f[j], f[j-v[i]]+w[i]);

(3) 多重背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<iostream>
#include<algorithm>
const int N = 1010;
int n, m;
int v[N], w[N], s[N], f[N][N];

int main(){
    cin >> n >> m;
    for(int i=1; i<=n; i++) cin >> v[i] >> w[i] >> s[i];

    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            for(int k=0; k*v[i]<=j && k<=s[i]; k++)
            f[i][j] = max(f[i][j], f[i-1][j-k*v[i]] + k*w[i]);
        }
    }
    cout << f[n][m];
}

优化后： 二进制优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// 注意全局const int变量值没明白
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 12010, M = 2010;
int v[N], w[N], s[N];
int f[M];
int n, m;

int main(){
    cin >> n >> m;
    int cnt = 0;
    for(int i=1; i<=n; i++){
        int a, b, c;
        cin >> a >> b >> c;

        int k=1;
        while(k<=c){
            cnt++;
            v[cnt]=k*a;
            w[cnt]=k*b;
            s-=k;
            k*=2;
        }
        if(c>0){
            cnt++;
            v[cnt]=c*a;
            w[cnt]=c*b;
        }
    }

    for(int i=1; i<=cnt; i++)
        for(int j=m; j>=w[i]; j--)
            f[j] = max(f[j], f[j-v[i]] + w[i]);

    cout << f[cnt];
}

(4) 分组背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<iostream>
#include<algorithm>
using namespace std;

const int N = 110;
int v[N][N], w[N][N], s[N];
int f[N];
int n, m;

int main(){
    cin >> n >> m;
    for(int i=1; i<=n; i++){
        cin >> s[i];
        for(int j=1; j<=s[i]; j++) cin >> v[i][j] >> w[i][j];
    }
        
    for(int i=1; i<=n; i++)
        for(int j=m; j>=0; j--)
            for(int k=1; k<=s[i]; k++)
                if(j>=v[i][k]) f[j] = max(f[j], f[j-v[i][k]] + w[i][k]);

    cout << f[m];    
}

线性DP

898.数字三角形

初始化范围注意

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<iostream>
using namespace std;
const int N = 510, INF = -1e9;
int a[N][N], f[N][N];
int n;

int main(){
    cin >> n;
    for(int i=1; i<=n; i++)
        for(int j=1; j<=i; j++)
            cin >> a[i][j];
    
    for(int i=0; i<=n; i++)
        for(int j=0; j<=i+1; j++)  // 注意这里！
            f[i][j] = INF;

    f[1][1] = a[1][1];
    for(int i=2; i<=n; i++)
        for(int j=1; j<=i; j++)
            f[i][j] = max(f[i-1][j], f[i-1][j-1]) + a[i][j];

    int res = INF;
    for(int i=1; i<=n; i++) res = max(res, f[n][i]);
    cout << res;
}

895.最长上升子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
const int N = 1010;
int a[N], f[N];
int n;
int main(){
	cin >> n;
	for(int i=1; i<=n; i++){
        cin >> a[i];
        f[i] = 1;
    } 
	
	for(int i=2; i<=n; i++)
		for(int j=1; j<i; j++)
			if(a[i] > a[j]) f[i] = max(f[i], f[j]+1);  //状态含义
		
	int res = 1;
	for(int i=1; i<=n; i++) res = max(res, f[i]);
	cout << res; 
}

优化：

另起炉灶：有点类似贪心思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
const int N = 100010;
int q[N], hh, tt;
int a[N], n;
int binary_search(int x, int l, int r){
    while(l < r){
        int mid = l + r >> 1;
        if(q[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return l;
}
int main(){
    cin >> n;
    for(int i=1; i<=n; i++) cin >> a[i];
    
    hh=0, tt=-1;
    for(int i=1; i<=n; i++){
        if(hh > tt)  q[++tt] = a[i]; // 空，直接加入
        else{
            if(q[tt] < a[i]) q[++tt] = a[i];
            else{
                int index = binary_search(a[i], hh, tt);
                q[index] = a[i];
            }
        }
    }
    cout << tt - hh + 1;
}

897.最长公共子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const int N = 1010;
int a[N], b[N], f[N][N];
int n, m;

int main(){
    cin >> n >> m >> a + 1 >> b + 1;

    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            f[i][j] = max(f[i][j-1], f[i-1][j]);
            if(a[i] == b[j]) f[i][j] = max(f[i][j], f[i-1][j-1]+1);
        }
    }
    cout << f[n][m];
}

899.编辑距离

我的错误思路：与最大公共子序列相关(?);

1

区间DP

  • 框架
1
2
3
4
// 外层区间长度循环；内层索引循环
for(len...){
    for(a...) //...
}

282.石子合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
const int N = 310;
int a[N], s[N], f[N][N];
int n;
int main(){
    cin >> n;
    for(int i=1; i<=n; i++){
        cin >> a[i];
        s[i] = a[i] + s[i-1];  // 注意求前缀和
    }

    memset(f, 0x3f, sizeof f);  // 1.
    for(int i=1; i<=n; i++) f[i][i] = 0; // 2.
    
    for(int len=2; len<=n; len++){
        for(int i=1; i+len-1<=n; i++){  // 3.
            int l=i, r=i+len-1;
            for(int k=l; k<=r; k++){
                f[l][r] = min(f[l][k]+f[k+1][r]+s[r]-s[l-1], f[l][r]);
            }
        }
    }
    cout << f[1][n];
}

计数类DP

338.计数问题

数位统计DP

状态压缩DP

树形DP

记忆化搜索

Powered by Hexo and Hexo-theme-hiker

Copyright © 2013 - 2022 Bowlmeat's Blogs All Rights Reserved.

访客数 : | 访问量 :